Circuits Électriques

Analyse d’un Circuit de Lissage d’Alimentation

Analyse d'un Circuit de Lissage d'Alimentation

Analyse d'un Circuit de Lissage d'Alimentation

Contexte : Le lissage capacitifTechnique utilisant un condensateur pour réduire les variations (ondulation) d'une tension continue redressée..

La plupart des appareils électroniques nécessitent une alimentation en tension continue (DC) stable pour fonctionner. Cependant, le réseau électrique fournit une tension alternative (AC). Le premier composant d'une alimentation est donc un transformateur (qui abaisse la tension) suivi d'un redresseurCircuit électronique qui convertit la tension alternative (AC) en tension continue pulsée (DC pulsé)., qui convertit l'AC en DC pulsé. Ce DC pulsé n'est pas stable et doit être "lissé". C'est le rôle du filtre de lissage, le plus simple étant un condensateur en parallèle de la charge.

Remarque Pédagogique : Cet exercice vous apprendra à analyser et dimensionner ce filtre capacitif simple. Vous calculerez la qualité de la tension DC obtenue en évaluant sa composante moyenne et son "ondulation" résiduelle.

Objectifs Pédagogiques

  • Comprendre le rôle d'un redresseur en pont et d'un filtre capacitif.
  • Calculer la tension de crête et la fréquence d'ondulation après un redressement double alternance.
  • Estimer la tension d'ondulation (ripple) crête-à-crête.
  • Déterminer la tension DC moyenne en sortie du filtre.

Données de l'étude

On étudie une alimentation linéaire simple. Le transformateur fournit une tension sinusoïdale de 12V efficaces (RMS) à 50 Hz. Cette tension est appliquée à un pont de diodes (redresseur double alternance). Un filtre RC est placé en sortie, avant la charge.

Fiche Technique
Caractéristique Valeur
Tension d'entrée AC (RMS) 12 V
Fréquence d'entrée AC 50 Hz
Chute de tension totale (pont de diodes) 1.4 V
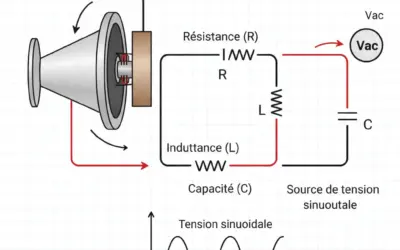
Schéma de principe du filtre de lissage
V_AC (RMS) 12V, 50Hz Pont Redresseur (~) (~) (+) (-) C R_charge V_in (redressée) V_out (lissée)
[Nom du Paramètre] [Description ou Formule] [Valeur] [Unité]
Capacité de Lissage C 1000 µF
Résistance de Charge R 100 Ω

Questions à traiter

  1. Calculer la tension de crête à la sortie du pont de diodes (avant le filtre).
  2. Déterminer la fréquence du signal redressé (fréquence d'ondulation).
  3. En utilisant l'approximation standard, calculer la tension d'ondulation crête-à-crête (\(V_r\)) aux bornes de la charge.
  4. Estimer la tension DC moyenne (\(V_{\text{DC,avg}}\)) aux bornes de la charge.
  5. Calculer le facteur d'ondulation (\(\gamma\)) en pourcentage, défini comme \(\gamma = (V_r / V_{\text{DC,avg}}) \times 100\%\).

Les bases du Lissage Capacitif

Pour convertir le courant alternatif (AC) en courant continu (DC) utilisable, on utilise deux étapes principales : le redressement et le filtrage (ou lissage).

1. Redressement Double Alternance
Un pont de diodes (redresseur double alternance) "retourne" les alternances négatives de la tension AC. La tension de sortie est toujours positive mais pulsée.

  • La tension de crête AC est : \(V_{\text{crête,AC}} = V_{\text{RMS}} \times \sqrt{2}\).
  • En sortie de pont, la tension de crête DC est : \(V_{\text{DC,crête}} = V_{\text{crête,AC}} - V_{\text{diodes}}\).
  • La fréquence de ces pulsations est le double de la fréquence AC : \(f_{\text{rect}} = 2 \times f_{\text{AC}}\).

2. Filtre Capacitif (Lissage)
Un condensateur (C) placé en parallèle de la charge (R) se charge rapidement à la tension de crête. Lorsque la tension redressée commence à chuter, le condensateur se décharge lentement dans la résistance, maintenant ainsi la tension à un niveau élevé. \[ V_{\text{ondulation}} \approx \frac{V_{\text{DC,crête}}}{f_{\text{rect}} \times R \times C} \] Cette approximation est valide si la constante de temps \(\tau = RC\) est bien plus grande que la période d'ondulation \(T_{\text{rect}} = 1/f_{\text{rect}}\).

Correction : Analyse d'un Circuit de Lissage d'Alimentation

Question 1 : Calculer la tension de crête à la sortie du pont de diodes (avant le filtre).

Principe

Pour trouver la tension de crête maximale que le condensateur "verra", nous devons d'abord trouver la tension de crête de la source AC (en utilisant la valeur RMS), puis soustraire la chute de tension causée par le pont de diodes (deux diodes sont toujours en conduction dans un pont).

Mini-Cours

La tension RMS (Root Mean Square) est la valeur "efficace" d'une tension AC. Pour un signal sinusoïdal, la valeur de crête (maximale) est \(\sqrt{2}\) fois plus grande que la valeur RMS. Chaque diode silicium standard introduit une chute de tension d'environ 0.7V lorsqu'elle conduit.

Remarque Pédagogique

N'oubliez jamais de convertir la tension RMS en tension de crête ! C'est l'erreur la plus fréquente. Le condensateur se charge à la valeur de crête, pas à la valeur RMS.

Normes

Nous utilisons les conventions standard de l'électronique : \(\sqrt{2} \approx 1.414\) et la chute de tension d'une diode au silicium est \(V_f \approx 0.7V\). Pour un pont, deux diodes conduisent en série, donc la chute totale est \(2 \times 0.7V = 1.4V\).

Formule(s)

Les deux formules clés pour cette étape.

Tension de crête AC

\[ V_{\text{crête,AC}} = V_{\text{RMS}} \times \sqrt{2} \]

Tension de crête DC (Sortie Redresseur)

\[ V_{\text{DC,crête}} = V_{\text{crête,AC}} - V_{\text{diodes}} \]
Hypothèses

Nous supposons que le transformateur et les diodes sont idéaux, à l'exception de la chute de tension directe de 1.4V pour le pont, qui est constante.

  • Le signal AC est parfaitement sinusoïdal.
  • La chute de tension des diodes est constante à 1.4V.
Donnée(s)

Les données pertinentes de l'énoncé pour cette question.

ParamètreSymboleValeurUnité
Tension AC Efficace\(V_{\text{RMS}}\)12V
Chute de tension du pont\(V_{\text{diodes}}\)1.4V
Astuces

Un moyen rapide de calculer \(\times \sqrt{2}\) est de multiplier par 1.414. Pour cet exercice, 12 * 1.414 = 16.97. C'est une bonne approximation.

Schéma (Avant les calculs)

Visualisation de la transformation de tension AC RMS en DC Crête.

De l'AC RMS au DC Crête
0V V_crête,AC = 16.97V V_DC,crête = 15.57V V_RMS = 12V V_diodes 1.4V
Calcul(s)

Suivons les deux étapes définies par les formules.

Étape 1 : Calcul de la tension de crête AC

\[ \begin{aligned} V_{\text{crête,AC}} &= 12 \text{ V} \times \sqrt{2} \\ &\approx 12 \times 1.4142 \\ &\approx 16.97 \text{ V} \end{aligned} \]

Maintenant, nous prenons cette valeur de crête AC (16.97 V) et nous soustrayons la chute de tension du pont de diodes (1.4 V) pour trouver la tension de crête réelle que le filtre recevra.

Étape 2 : Calcul de la tension de crête DC (après redressement)

\[ \begin{aligned} V_{\text{DC,crête}} &= V_{\text{crête,AC}} - V_{\text{diodes}} \\ &= 16.97 \text{ V} - 1.4 \text{ V} \\ &= 15.57 \text{ V} \end{aligned} \]

C'est la valeur maximale que le condensateur atteindra. Nous utiliserons 15.57 V comme notre \(V_{\text{DC,crête}}\) pour la suite.

Schéma (Après les calculs)

Le résultat est la tension maximale que le condensateur de lissage pourra atteindre.

Tension Maximale en Sortie de Pont
0V V_DC,crête ≈ 15.57 V Tension redressée (DC pulsé)
Réflexions

La tension de 15.57V est le point de départ de notre analyse de lissage. C'est la tension maximale que l'alimentation peut fournir avant que le condensateur n'entre en jeu. Notez qu'elle est significativement plus élevée que la tension RMS de 12V, un fait important pour le dimensionnement des composants.

Points de vigilance

Ne pas confondre \(V_{\text{RMS}}\), \(V_{\text{crête,AC}}\) et \(V_{\text{DC,crête}}\). Chacune a une valeur et une signification distincte. Oublier la chute de tension des diodes est aussi une erreur courante qui fausse tous les calculs suivants.

Points à retenir

Pour un redresseur en pont (double alternance) :

  • \(V_{\text{crête,AC}} = V_{\text{RMS}} \times \sqrt{2}\)
  • \(V_{\text{DC,crête}} = V_{\text{crête,AC}} - 1.4V\)
Le saviez-vous ?

Dans les alimentations à découpage modernes (comme les chargeurs de téléphone), le lissage se fait à très haute fréquence (des dizaines ou centaines de kHz), ce qui permet d'utiliser des condensateurs beaucoup plus petits et moins chers pour obtenir une tension DC très stable !

FAQ

Questions fréquentes sur cette étape.

Pourquoi 1.4V et pas 0.7V ?

Dans un pont de diodesCircuit redresseur utilisant quatre diodes pour convertir les deux alternances d'un signal AC en DC pulsé., le courant doit toujours traverser *deux* diodes en série pour compléter le circuit (par exemple, D1 et D2 pour l'alternance positive, D3 et D4 pour la négative). La chute de tension totale est donc \(0.7V + 0.7V = 1.4V\).

Cette chute de 1.4V est-elle toujours constante ?

En réalité, non. C'est une simplification. La chute de tension d'une diode varie légèrement avec le courant qui la traverse. Cependant, pour l'analyse de circuits d'alimentation, la considérer comme constante est une approximation très juste et largement suffisante.

Résultat Final
La tension de crête à la sortie du pont de diodes est de 15.57 V.
A vous de jouer

Que deviendrait \(V_{\text{DC,crête}}\) si la tension d'entrée RMS était de 9V ?

Mini Fiche Mémo

Synthèse de la Question 1 :

  • Concept Clé : Conversion RMS -> Crête et chute de tension des diodes.
  • Formule Essentielle : \(V_{\text{DC,crête}} = (V_{\text{RMS}} \times \sqrt{2}) - 1.4V\).
  • Point de Vigilance Majeur : Ne pas oublier les 1.4V de chute.

Question 2 : Déterminer la fréquence du signal redressé (fréquence d'ondulation).

Principe

Nous devons déterminer à quelle fréquence la tension redressée "pulse" ou se répète. Un redresseur double alternance, comme le pont de diodes, utilise les *deux* moitiés (positive et négative) du cycle AC d'entrée. Il "retourne" l'alternance négative pour la rendre positive. Par conséquent, nous obtenons deux pics positifs de tension pendant la durée d'un seul cycle AC d'origine.

Mini-Cours

C'est une distinction fondamentale en redressement :

  • Redressement Simple Alternance : Une seule diode est utilisée. Elle bloque l'alternance négative. On obtient un pic de tension, suivi d'un "trou" (0V). La fréquence de sortie est donc la *même* que l'entrée. (\(f_{\text{rect}} = f_{\text{AC}}\))
  • Redressement Double Alternance : Un pont de 4 diodes est utilisé. Il "retourne" l'alternance négative. On obtient deux pics de tension positifs successifs. La fréquence de sortie est donc le *double* de l'entrée. (\(f_{\text{rect}} = 2 \times f_{\text{AC}}\))

Remarque Pédagogique

Ce doublement de la fréquence est un avantage majeur. La période (le temps) entre deux pics est divisée par deux (de 20ms à 10ms pour du 50Hz). Le condensateur de lissage a donc beaucoup moins de temps pour se décharger, ce qui réduit considérablement l'ondulation et facilite le filtrage.

Normes

Ceci n'est pas une "norme" (comme un Eurocode), mais une loi fondamentale et une conséquence directe de l'analyse de Fourier appliquée aux circuits redresseurs.

Formule(s)

Fréquence de sortie (Double Alternance)

\[ f_{\text{rect}} = 2 \times f_{\text{AC}} \]

Période d'ondulation

\[ T_{\text{rect}} = \frac{1}{f_{\text{rect}}} = \frac{1}{2 \times f_{\text{AC}}} \]
Hypothèses

Aucune hypothèse supplémentaire n'est nécessaire. C'est une conséquence directe du type de redresseur (double alternance).

Donnée(s)

La seule donnée de l'énoncé nécessaire pour cette question.

ParamètreSymboleValeurUnité
Fréquence AC d'Entrée\(f_{\text{AC}}\)50Hz
Astuces

Visualisez-le : Un cycle AC à 50 Hz dure \(T = 1/50 = 0.02s = 20 \text{ ms}\). Durant ces 20 ms, il y a une alternance positive et une négative. Le pont redresseur transforme les deux en pics positifs. La nouvelle période (le temps entre les pics) est donc de 10 ms. La nouvelle fréquence est \(f = 1 / 10 \text{ ms} = 1 / 0.01 \text{ s} = 100 \text{ Hz}\).

Schéma (Avant les calculs)

Visualisation du doublement de la fréquence par le redresseur double alternance.

Doublement de la Fréquence
Signal d'Entrée (AC) 1 Cycle (T_AC = 20ms) Signal Redressé (DC Pulsé) T_rect = 10ms
Calcul(s)

On applique directement la formule du redresseur double alternance.

Étape 1 : Application de la formule

\[ \begin{aligned} f_{\text{rect}} &= 2 \times f_{\text{AC}} \\ &= 2 \times 50 \text{ Hz} \\ &= 100 \text{ Hz} \end{aligned} \]

Cette valeur de 100 Hz est la fréquence d'ondulation que le filtre RC devra atténuer.

Schéma (Après les calculs)

Le schéma "Avant les calculs" illustre déjà parfaitement ce résultat. Le signal d'entrée a une période (T) de 20ms, tandis que le signal de sortie a une période (\(T_{\text{rect}}\)) de 10ms, correspondant à une fréquence de 100 Hz.

Réflexions

Cette fréquence de 100 Hz est cruciale. C'est la fréquence de l'"ondulation" que nous allons devoir filtrer. Le condensateur n'aura que 10ms (\(T_{\text{rect}} = 1/100 \text{ Hz}\)) entre chaque pic pour se décharger. C'est cette valeur que nous utiliserons dans la formule de l'ondulation à la question 3.

Points de vigilance

Le piège principal est d'oublier de doubler la fréquence. Si vous utilisez 50 Hz dans les calculs suivants, votre estimation de l'ondulation (Vr) sera fausse (elle sera deux fois plus grande, ce qui est pessimiste mais incorrect).

Points à retenir

Si vous ne deviez retenir que deux points clés :

  • Redressement Simple Alternance : \(f_{\text{out}} = f_{\text{in}}\)
  • Redressement Double Alternance : \(f_{\text{out}} = 2 \times f_{\text{in}}\)
Le saviez-vous ?

Dans les systèmes d'alimentation triphasés (très courants dans l'industrie), un redressement double alternance (avec un pont de 6 diodes) produit une fréquence d'ondulation de \(6 \times f_{\text{in}}\). Pour 50 Hz en entrée, l'ondulation est à 300 Hz, avec une amplitude beaucoup plus faible, la rendant encore plus facile à filtrer !

FAQ

Questions fréquentes sur cette étape.

Pourquoi la fréquence double-t-elle ?

Le signal AC a un pic positif à 5ms et un pic négatif à 15ms (pour un cycle de 20ms). Le redresseur transforme le pic négatif de 15ms en un pic positif. L'onde de sortie a donc des pics à 5ms ET à 15ms. L'intervalle entre les pics n'est plus que de 10ms, ce qui correspond à une fréquence de 100 Hz.

Est-ce que cela change la tension de crête ?

Non. Le doublement de la fréquence ne change pas l'amplitude (la tension de crête) du signal, qui est toujours déterminée par la tension d'entrée AC et la chute des diodes (calculée à la Q1).

Résultat Final
La fréquence du signal redressé (fréquence d'ondulation) est de 100 Hz.
A vous de jouer

Si cette alimentation était utilisée aux États-Unis, où la fréquence du réseau est de 60 Hz, quelle serait la nouvelle fréquence d'ondulation ?

Mini Fiche Mémo

Synthèse de la Question 2 :

  • Concept Clé : Le redressement double alternance double la fréquence.
  • Formule Essentielle : \(f_{\text{rect}} = 2 \times f_{\text{AC}}\).
  • Point de Vigilance Majeur : Ne pas confondre avec le redressement simple alternance (\(f = f_{\text{AC}}\)).

Question 3 : Calculer la tension d'ondulation crête-à-crête (\(V_r\)) aux bornes de la charge.

Principe

L'ondulation (\(V_r\)) est la petite variation de tension causée par la décharge du condensateur dans la résistance entre deux pics de tension redressée. Nous pouvons l'estimer en supposant que le condensateur se décharge à un courant (presque) constant pendant la courte période entre les pics.

Mini-Cours

La décharge d'un condensateur est \(Q = C \times V\). Le courant est \(I = dQ/dt\). En approximant : \(\Delta Q = C \times \Delta V\). Si on suppose un courant de décharge constant \(I_{\text{DC}}\), alors \(\Delta Q = I_{\text{DC}} \times \Delta t\). Ici, \(\Delta V = V_r\) (l'ondulation) et \(\Delta t = T_{\text{rect}} = 1/f_{\text{rect}}\). Donc \(C \times V_r \approx I_{\text{DC}} \times T_{\text{rect}}\). Comme \(I_{\text{DC}} \approx V_{\text{DC,avg}} / R \approx V_{\text{DC,crête}} / R\) (en première approximation), on a : \(C \times V_r \approx (V_{\text{DC,crête}} / R) \times (1 / f_{\text{rect}})\). En réarrangeant, on obtient la formule d'approximation standard.

Remarque Pédagogique

Cette formule d'approximation est le cœur du dimensionnement des filtres. Elle relie l'ondulation (ce que l'on veut minimiser) aux trois composants que l'on peut choisir : C (capacité), R (charge) et f (fréquence).

Normes

Ceci est une approximation standard en ingénierie, non une loi fondamentale. Elle est très précise tant que l'ondulation est faible par rapport à la tension de crête (ce qui est le but !).

Formule(s)

Approximation de l'Ondulation (Ripple)

\[ V_{r} \approx \frac{V_{\text{DC,crête}}}{f_{\text{rect}} \times R \times C} \]
Hypothèses

L'hypothèse clé pour cette formule est que la constante de temps \(\tau = RC\) est bien plus grande que la période d'ondulation \(T_{\text{rect}}\). Calculons : \(\tau = 100 \Omega \times 1000 \mu F = 100 \times 0.001 = 0.1 \text{ s}\). \(T_{\text{rect}} = 1 / 100 \text{ Hz} = 0.01 \text{ s}\). Puisque \(0.1 \text{ s} \gg 0.01 \text{ s}\) (10 fois plus grand), notre hypothèse est valide.

  • \(\tau \gg T_{\text{rect}}\) (Constante de temps de décharge longue).
  • La décharge est supposée linéaire (courant constant).
Donnée(s)

Nous avons besoin de toutes les données calculées et fournies.

ParamètreSymboleValeurUnité
Tension DC Crête\(V_{\text{DC,crête}}\)15.57V
Fréquence Redressée\(f_{\text{rect}}\)100Hz
Résistance de ChargeR100Ω
Capacité de LissageC1000µF
Astuces

Attention aux unités ! La capacité doit être en Farads (F), pas en microfarads (µF). \(1000 \text{ µF} = 1000 \times 10^{-6} \text{ F} = 0.001 \text{ F}\).

Schéma (Avant les calculs)

Visualisation de la tension d'ondulation (Vr) sur la tension de sortie.

Tension d'Ondulation (Ripple)
0V V_DC,crête V_min V_r
Calcul(s)

Suivons les étapes pour appliquer la formule d'approximation.

Étape 1 : Conversion de la capacité

\[ C = 1000 \text{ µF} = 1000 \times 10^{-6} \text{ F} = 0.001 \text{ F} \]

Nous avons maintenant toutes les valeurs pour la formule \( V_{r} \approx \frac{V_{\text{DC,crête}}}{f_{\text{rect}} \times R \times C} \).
- \(V_{\text{DC,crête}} = 15.57 \text{ V}\) (de la Q1)
- \(f_{\text{rect}} = 100 \text{ Hz}\) (de la Q2)
- \(R = 100 \text{ } \Omega\)
- \(C = 0.001 \text{ F}\)

Étape 2 : Calcul du dénominateur (\(f_{\text{rect}} \times R \times C\))

\[ f_{\text{rect}} \times R \times C = 100 \text{ Hz} \times 100 \text{ } \Omega \times 0.001 \text{ F} = 10 \]

Ce terme (10) est sans dimension (car \(f \times (R \times C) \rightarrow s^{-1} \times s = 1\)).

Étape 3 : Calcul final de \(V_r\)

Maintenant, nous divisons la tension de crête par ce terme :

\[ V_{r} \approx \frac{V_{\text{DC,crête}}}{10} = \frac{15.57 \text{ V}}{10} = 1.557 \text{ V} \]
Schéma (Après les calculs)

Le schéma "Avant les calculs" est déjà annoté avec le résultat. L'ondulation crête-à-crête est de 1.557V.

Réflexions

Une ondulation de 1.557V sur une tension de 15.57V est notable (environ 10%). Pour de nombreux appareils électroniques (comme un amplificateur audio), c'est beaucoup trop. Pour un simple chargeur de batterie, cela pourrait être acceptable. Cela montre que nos valeurs de R et C ne sont peut-être pas optimales pour une alimentation de haute qualité.

Points de vigilance

L'erreur la plus commune est la gestion des unités. Assurez-vous que C est en Farads, R en Ohms, f en Hertz. Le produit \(f \times R \times C\) est un nombre sans dimension (car \(1/f\) est en secondes et \(RC\) est en secondes).

Points à retenir
  • La tension d'ondulation \(V_r\) est inversement proportionnelle à C, R, et f.
  • Pour réduire l'ondulation, il faut augmenter la capacité (C) ou la résistance de charge (R) (c'est-à-dire réduire le courant demandé).
Le saviez-vous ?

Les très grosses alimentations de laboratoire ou industrielles utilisent parfois des filtres "LC" (Inductance-Capacité) ou "Pi" (C-L-C), qui sont bien plus efficaces pour éliminer l'ondulation que de simples filtres RC.

FAQ

...

Cette formule est-elle toujours précise ?

Non, c'est une approximation. La décharge n'est pas linéaire mais exponentielle (\(V(t) = V_{\text{crête}} \cdot e^{-t/RC}\)). Cependant, comme \(\tau \gg T_{\text{rect}}\), la première partie de l'exponentielle est presque une ligne droite, donc l'approximation est excellente (souvent à 1-2% près).

Résultat Final
La tension d'ondulation crête-à-crête (Vr) est d'environ 1.557 V.
A vous de jouer

Que deviendrait \(V_r\) si on utilisait un condensateur de 4700 µF ?

Mini Fiche Mémo

Synthèse de la Question 3 :

  • Concept Clé : Approximation de l'ondulation par décharge du condensateur.
  • Formule Essentielle : \(V_r \approx V_{\text{crête}} / (f \cdot R \cdot C)\).
  • Point de Vigilance Majeur : Unités ! C doit être en Farads.

Question 4 : Estimer la tension DC moyenne (\(V_{\text{DC,avg}}\)) aux bornes de la charge.

Principe

La tension de sortie n'est pas une ligne droite, elle oscille entre \(V_{\text{DC,crête}}\) et \(V_{\text{min}} = V_{\text{DC,crête}} - V_r\). La tension moyenne, que lirait un voltmètre en mode DC, se situe approximativement au milieu de cette ondulation.

Mini-Cours

L'ondulation est (approximativement) une forme d'onde en "dent de scie" qui se superpose à la tension DC. La valeur moyenne d'une dent de scie est à mi-chemin entre son pic et son creux. Par conséquent, la tension DC moyenne est la tension de crête moins la moitié de l'ondulation crête-à-crête.

Remarque Pédagogique

C'est cette tension \(V_{\text{DC,avg}}\) qui est la "vraie" tension DC de sortie de l'alimentation. C'est la valeur la plus importante pour l'appareil qui sera alimenté.

Normes

C'est une approximation géométrique (la moyenne d'une dent de scie) appliquée à notre signal.

Formule(s)

Tension DC Moyenne

\[ V_{\text{DC,avg}} \approx V_{\text{DC,crête}} - \frac{V_r}{2} \]
Hypothèses

Nous supposons que l'ondulation est symétrique (en forme de dent de scie ou triangulaire), ce qui est une bonne approximation pour notre cas.

Donnée(s)

Nous utilisons les résultats des questions 1 et 3.

ParamètreSymboleValeurUnité
Tension DC Crête\(V_{\text{DC,crête}}\)15.57V
Tension d'Ondulation\(V_r\)1.557V
Astuces

Ne divisez pas \(V_{\text{DC,crête}}\) par deux. La tension moyenne est proche du pic, pas de la moitié du pic. On soustrait juste la *moitié de l'ondulation*.

Schéma (Avant les calculs)

Localisation de la tension moyenne sur le graphique de l'ondulation.

Localisation de V_avg
V_DC,crête V_min V_DC,avg (Niveau moyen de la tension)
Calcul(s)

Étape 1 : Calcul de la moitié de l'ondulation

\[ \frac{V_r}{2} = \frac{1.557 \text{ V}}{2} = 0.7785 \text{ V} \]

Maintenant, nous soustrayons cette 'demi-ondulation' (0.7785 V) de la tension de crête maximale (15.57 V) pour trouver la valeur moyenne.

Étape 2 : Calcul de la tension moyenne

\[ \begin{aligned} V_{\text{DC,avg}} &\approx V_{\text{DC,crête}} - \frac{V_r}{2} \\ &= 15.57 \text{ V (de Q1)} - 0.7785 \text{ V (de l'Étape 1)} \\ &\approx 14.7915 \text{ V} \end{aligned} \]

Nous arrondirons à 14.79 V pour le calcul suivant.

Schéma (Après les calculs)

Le schéma "Avant les calculs" est déjà correct, avec \(V_{\text{DC,avg}}\) positionné à environ 14.79V.

Réflexions

La tension moyenne de 14.79V est la tension "utile" fournie à la charge. Notez qu'elle est inférieure à la tension de crête de 15.57V. Cette différence est due à l'ondulation. Moins il y a d'ondulation, plus \(V_{\text{DC,avg}}\) sera proche de \(V_{\text{DC,crête}}\).

Points de vigilance

Attention à ne pas utiliser la formule \(V_{\text{DC,avg}} = 0.636 \times V_{\text{crête}}\). Cette formule est valable pour un signal redressé *non filtré*. L'ajout du condensateur change radicalement la forme du signal et donc sa valeur moyenne.

Points à retenir
  • La tension DC moyenne d'un signal filtré est la tension de crête moins la moitié de l'ondulation crête-à-crête.
Le saviez-vous ?

Les multimètres numériques en mode "DC" mesurent cette tension moyenne (\(V_{\text{DC,avg}}\)). Si vous passez en mode "AC", ils essaieront de mesurer la composante alternative (l'ondulation), mais le résultat (RMS) sera différent de notre \(V_r\) crête-à-crête.

FAQ

...

Est-ce la seule façon de calculer la moyenne ?

C'est la plus simple et la plus courante. Le calcul exact nécessiterait d'intégrer la forme d'onde (charge et décharge exponentielle) sur une période, ce qui est beaucoup plus complexe et n'apporte qu'une précision minime dans la plupart des cas.

Résultat Final
La tension DC moyenne (V_DC_avg) est d'environ 14.79 V.
A vous de jouer

En utilisant le résultat de "A vous de jouer" de la Q3 (\(V_r \approx 0.331V\) pour C=4700µF), quelle serait la nouvelle tension moyenne ?

Mini Fiche Mémo

Synthèse de la Question 4 :

  • Concept Clé : La tension moyenne est la tension de crête moins la moitié de l'ondulation.
  • Formule Essentielle : \(V_{\text{DC,avg}} \approx V_{\text{DC,crête}} - (V_r / 2)\).

Question 5 : Calculer le facteur d'ondulation (\(\gamma\)) en pourcentage.

Principe

Le facteur d'ondulation est une mesure de la "qualité" de la tension continue. Il exprime l'amplitude de l'ondulation (la composante AC résiduelle) en pourcentage de la tension moyenne (la composante DC utile). Un faible pourcentage signifie un lissage de haute qualité.

Mini-Cours

Il existe plusieurs définitions du facteur d'ondulation (parfois en utilisant les valeurs RMS). Pour cet exercice, nous utilisons une définition simple et pratique : le rapport de l'ondulation crête-à-crête à la tension moyenne. Plus ce ratio est proche de zéro, plus la sortie ressemble à une ligne DC parfaite.

Remarque Pédagogique

C'est un chiffre très parlant. Dire "l'ondulation est de 1.5V" est moins informatif que de dire "l'ondulation est de 10%". 1.5V d'ondulation sur une sortie de 15V (10%) est mauvais, mais 1.5V sur une sortie de 1000V (0.15%) serait excellent.

Normes

C'est une métrique de performance standard pour les alimentations électriques.

Formule(s)

Facteur d'Ondulation (en %)

\[ \gamma \text{ (en %)} = \frac{V_r}{V_{\text{DC,avg}}} \times 100\% \]
Hypothèses

Aucune nouvelle hypothèse. Nous utilisons simplement les valeurs calculées précédemment.

Donnée(s)

Nous utilisons les résultats finaux des questions 3 et 4.

ParamètreSymboleValeurUnité
Tension d'Ondulation\(V_r\)1.557V
Tension DC Moyenne\(V_{\text{DC,avg}}\)14.79V
Astuces

Assurez-vous d'utiliser les deux valeurs calculées (Vr et V_avg) et non les valeurs de crête. C'est le rapport de "ce qui est mauvais" (Vr) sur "ce qui est bon" (\(V_{\text{avg}}\)).

Schéma (Avant les calculs)

Ce calcul est une métrique, il n'a pas de schéma direct autre que ceux déjà vus, qui comparent visuellement \(V_r\) et \(V_{\text{DC,avg}}\).

Calcul(s)

Nous utilisons les résultats finaux des questions 3 et 4 :
- \(V_r = 1.557 \text{ V}\) (Ondulation)
- \(V_{\text{DC,avg}} = 14.79 \text{ V}\) (Moyenne utile)

Étape 1 : Calcul du ratio

\[ \text{Ratio} = \frac{V_r}{V_{\text{DC,avg}}} = \frac{1.557 \text{ V}}{14.79 \text{ V}} \approx 0.1052 \]

Ce ratio de 0.1052 signifie que l'ondulation représente environ 10.5% de la tension moyenne. Pour l'exprimer en pourcentage, on multiplie par 100.

Étape 2 : Conversion en pourcentage

\[ \begin{aligned} \gamma &= 0.1052 \times 100\% \\ &= 10.52 \% \end{aligned} \]
Schéma (Après les calculs)

Non applicable pour ce calcul de métrique.

Réflexions

Un facteur d'ondulation de 10.5% est assez élevé. Une alimentation de "bonne" qualité visera souvent un facteur d'ondulation inférieur à 1% ou 2%. Notre circuit n'est pas très performant, principalement parce que la résistance de charge (100Ω) demande un courant relativement élevé (\(I \approx 14.79V / 100\Omega \approx 148mA\)) pour le condensateur de 1000µF.

Points de vigilance

Ne pas inverser le rapport (ne pas faire \(V_{\text{avg}} / V_r\)). Le facteur d'ondulation doit être petit pour un bon filtre.

Points à retenir
  • Le facteur d'ondulation \(\gamma = V_r / V_{\text{DC,avg}}\) est la métrique clé pour juger la qualité d'un lissage.
  • Plus \(\gamma\) est faible, meilleur est le lissage.
Le saviez-vous ?

Pour obtenir des facteurs d'ondulation très faibles (ex: < 0.01%), on ajoute un "régulateur de tension" (comme un LM7812) après le filtre. Ce composant actif maintient la tension de sortie parfaitement stable, absorbant activement l'ondulation résiduelle.

FAQ

...

10.5% c'est bon ou mauvais ?

Cela dépend de l'application. Pour alimenter une LED, c'est parfait. Pour alimenter un microprocesseur ou un préamplificateur audio, c'est catastrophique et causerait des dysfonctionnements ou un bruit horrible ("hum" de 100 Hz).

Résultat Final
Le facteur d'ondulation (\(\gamma\)) est d'environ 10.5 %.
A vous de jouer

En utilisant les résultats de "A vous de jouer" des Q3 et Q4 (\(V_r \approx 0.331V\), \(V_{\text{avg}} \approx 15.40V\)), quel est le nouveau facteur d'ondulation ?

Mini Fiche Mémo

Synthèse de la Question 5 :

  • Concept Clé : Métrique de qualité du lissage.
  • Formule Essentielle : \(\gamma \% = (V_r / V_{\text{DC,avg}}) \times 100\).

Outil Interactif : Simulateur de Filtre RC

Utilisez les curseurs pour voir l'influence de la Capacité (C) et de la Résistance (R) sur la qualité du lissage. (Basé sur V_crête = 15.57V et f = 100 Hz).

Paramètres d'Entrée
1000 µF
100 Ω
Résultats Clés
Tension d'ondulation (Vr) [V] -
Tension moyenne (V_avg) [V] -

Quiz Final : Testez vos connaissances

1. Un redresseur en pont de diodes (double alternance) :

2. Si la fréquence du signal AC d'entrée est de 50 Hz, la fréquence d'ondulation après un redresseur double alternance est :

3. Pour *réduire* la tension d'ondulation (améliorer le lissage), je dois :

4. Si la résistance de charge R *augmente* (ce qui signifie que la charge demande *moins* de courant) :

5. La tension DC moyenne (\(V_{\text{DC,avg}}\)) en sortie d'un filtre capacitif est :

Glossaire

Facteur d'Ondulation (\(\gamma\))
Une mesure (souvent en %) de l'amplitude de la composante AC résiduelle (ondulation) par rapport à la composante DC moyenne. Plus il est faible, meilleure est la qualité du lissage.
Lissage Capacitif
Technique utilisant un condensateur en parallèle de la charge pour "lisser" une tension DC pulsée en se chargeant lors des pics et en se déchargeant lentement entre les pics.
Pont de Diodes (Redresseur)
Un circuit à quatre diodes qui convertit un signal AC (double alternance) en un signal DC pulsé (unidirectionnel).
Tension d'Ondulation (Ripple, \(V_r\))
La variation périodique (crête-à-crête) de la tension DC en sortie d'un filtre de lissage. C'est la composante AC indésirable qui "survit" au filtrage.
Tension Efficace (RMS)
La valeur quadratique moyenne (Root Mean Square) d'un signal alternatif. Elle représente la valeur de tension DC qui produirait la même puissance de chauffage dans une résistance.
Analyse d'un Circuit de Lissage d'Alimentation

D’autres exercices de Régime SinusoÏdal:

Analyse d’un Déphaseur RC
Analyse d’un Déphaseur RC

Analyse d'un Déphaseur RC Analyse d'un Déphaseur : Circuit RC Contexte : Le Régime Sinusoïdal ForcéL'étude des circuits électriques alimentés par une source de tension ou de courant qui varie de manière sinusoïdale (comme le courant domestique).. En électronique, il...

0 commentaires
Soumettre un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *