Dans une chaîne de production automatisée, un tapis roulant doit maintenir une vitesse constante quelle que soit la charge transportée. Le système est propulsé par un moteur à courant continu (MCC). Pour garantir la performance, nous mettons en place une Boucle FerméeSystème où la sortie est mesurée et comparée à la consigne pour ajuster la commande. avec un correcteur proportionnel. L'objectif est d'étudier le comportement transitoire du système lors d'un démarrage (réponse indicielle).

Remarque Pédagogique : Cet exercice combine la modélisation physique (équations électriques et mécaniques) et l'automatique (fonctions de transfert et schémas blocs) pour dimensionner un asservissement.

Objectifs Pédagogiques

Modéliser un moteur à courant continu sous forme de schéma-bloc.
Déterminer la fonction de transfert en boucle ouverte (FTBO) et en boucle fermée (FTBF).
Calculer la constante de temps du système asservi.
Analyser l'influence du gain du correcteur sur la rapidité et la précision.

Données de l'étude

Le moteur est commandé par une tension d'induit \(u(t)\). La vitesse de rotation est notée \(\Omega(t)\). On néglige l'inductance de l'induit devant la résistance (constante de temps électrique négligeable devant la mécanique).

Fiche Technique du Moteur

Paramètre	Symbole	Valeur	Unité
Résistance d'induit	\(R\)	2.0	\(\Omega\)
Constante de couple / FEM	\(K\)	0.1	\(V \cdot \text{s}/\text{rad}\) ou \(N \cdot \text{m}/\text{A}\)
Moment d'inertie total	\(J\)	0.01	\(\text{kg} \cdot \text{m}^2\)
Coefficient de frottement	\(f\)	0.001	\(N \cdot \text{m} \cdot \text{s}/\text{rad}\)

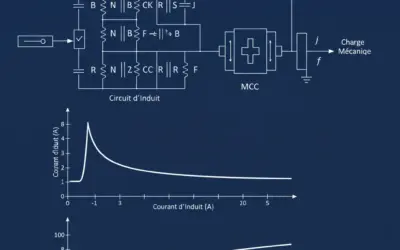
Schéma Fonctionnel de l'Asservissement

Questions à traiter

Établir les équations différentielles du moteur.
Déterminer la fonction de transfert en boucle ouverte (Moteur seul).
Calculer la fonction de transfert en boucle fermée avec le correcteur \(K_{\text{p}}\).
Déterminer la constante de temps et l'erreur statique du système asservi.
Tracer l'allure de la réponse indicielle.

Les bases théoriques

Pour modéliser le système, nous utilisons les lois fondamentales de l'électromagnétisme et de la mécanique, transformées dans le domaine de Laplace pour manipuler des équations algébriques simples.

Loi électrique de l'induit
En négligeant l'inductance, la tension aux bornes du moteur est la somme de la chute de tension résistive et de la force contre-électromotrice (FCEM).

Équation électrique

u(t) = R \cdot i(t) + e(t)

Avec \(e(t) = K \cdot \Omega(t)\) (FCEM proportionnelle à la vitesse).

Loi mécanique (PFD en rotation)
Le couple moteur doit vaincre l'inertie, les frottements et le couple résistant (ici nul à vide).

Équation mécanique

J \frac{\text{d}\Omega(t)}{\text{d}t} + f \cdot \Omega(t) = C_{\text{m}}(t)

Avec \(C_{\text{m}}(t) = K \cdot i(t)\) (Couple proportionnel au courant).

Formule de Black
Permet de calculer la fonction de transfert en boucle fermée (FTBF) à partir de la boucle ouverte (FTBO) et de la chaîne de retour (B).

Formule de Black

H_{\text{BF}}(p) = \frac{\text{Chaîne Directe}}{1 + \text{Chaîne Directe} \times \text{Retour}}

Correction : Asservissement de Vitesse d'un Moteur à Courant Continu

Question 1 : Équations Différentielles

Principe

Nous combinons les équations électrique et mécanique pour éliminer le courant \(i(t)\) et obtenir une relation directe entre la tension d'entrée \(u(t)\) et la vitesse de sortie \(\Omega(t)\). Cette étape est fondamentale pour construire la fonction de transfert.

Mini-Cours

Le Principe Fondamental de la Dynamique (PFD) en rotation stipule que la somme des couples est égale au produit de l'inertie par l'accélération angulaire : \(\sum C = J \dot{\Omega}\). Ici, le couple moteur \(K i(t)\) s'oppose au couple de frottement \(f \Omega(t)\).

Remarque Pédagogique

Le terme \(K^2/R\) qui apparaîtra dans l'équation finale agit comme un "frottement électromagnétique" supplémentaire. Plus le champ magnétique (lié à K) est fort, plus le moteur résiste naturellement au changement de vitesse, ce qui stabilise le système.

Normes

Les notations respectent la norme IEC 60027-1 pour les grandeurs électromagnétiques et IEC 60034 pour les machines tournantes.

Formule(s)

Formules de base

Loi des mailles & PFD

u = Ri + K\Omega \quad ; \quad J\dot{\Omega} + f\Omega = Ki

Hypothèses

On suppose pour ce modèle :

Inductance \(L\) de l'induit négligeable devant \(R\).
Arbre moteur parfaitement rigide (pas de torsion).
Frottements secs négligés (modèle visqueux pur).

Donnée(s)

Paramètre	Symbole	Unité SI
Constante de couple	\(K\)	N.m/A
Constante de FEM	\(K\)	V.s/rad

Astuces

Astuce mathématique : Isoler \(i(t)\) dans l'équation électrique est souvent plus simple que l'inverse car l'équation mécanique contient une dérivée, ce qui éviter d'avoir à intégrer.

Schéma Avant (Modèle Séparé)

Systèmes découplés

Calculs

Expression du courant

On exprime le courant \(i(t)\) à partir de l'équation électrique \(u(t) = Ri(t) + e(t)\) :

\begin{aligned} Ri(t) &= u(t) - e(t) \\ i(t) &= \frac{u(t) - K \Omega(t)}{R} \end{aligned}

Substitution

On remplace \(i(t)\) dans l'équation mécanique \(J\dot{\Omega} + f\Omega = Ki\) :

J \frac{\text{d}\Omega}{\text{d}t} + f \Omega = K \left( \frac{u - K \Omega}{R} \right)

Arrangement final

On distribue le K et on multiplie toute l'équation par R pour supprimer la fraction :

\begin{aligned} R \left( J \frac{\text{d}\Omega}{\text{d}t} + f \Omega \right) &= K(u - K\Omega) \\ RJ \frac{\text{d}\Omega}{\text{d}t} + Rf\Omega &= Ku - K^2\Omega \end{aligned}

On regroupe les termes en \(\Omega\) à gauche :

RJ \frac{\text{d}\Omega}{\text{d}t} + (Rf + K^2)\Omega(t) = Ku(t)

Schéma Après (Modèle Couplé)

Modèle Électromécanique Unifié

Réflexions

On obtient une équation différentielle linéaire du premier ordre à coefficients constants. Cela signifie que la réponse du système sera exponentielle, sans oscillation.

Points de vigilance

Attention aux unités de \(K\) : En unités SI, la valeur numérique de \(K_e\) (V.s/rad) est strictement égale à celle de \(K_c\) (N.m/A), c'est pourquoi on utilise un seul \(K\). Si vous utilisiez des tours/minute, cela ne marcherait plus !

Points à Retenir

L'essentiel :

L'équation couple les domaines électrique et mécanique via \(K\).
L'ordre du système est 1 (car L est négligé), sinon ce serait un ordre 2.

Le saviez-vous ?

Ce modèle simplifié est utilisé tel quel dans 90% des contrôleurs de servomoteurs industriels bas de gamme, car il est suffisant pour des dynamiques lentes.

FAQ

Pourquoi négliger l'inductance ?

Car la constante de temps électrique \(\tau_e = L/R\) est souvent 10 à 100 fois plus petite que la constante de temps mécanique. L'effet de L s'amortit très vite devant l'inertie.

Équation : \(R J \dot{\Omega} + (R f + K^2) \Omega = K u\)

A vous de jouer
Si \(K=0\) (pas de champ magnétique), que devient l'équation ?

📝 Mémo
Une seule équation pour tout gouverner.

Question 2 : Fonction de Transfert Boucle Ouverte (FTBO)

Principe

Le passage dans le domaine de Laplace permet de transformer l'équation différentielle en une équation algébrique simple pour obtenir le rapport Sortie/Entrée \(\Omega(p)/U(p)\).

Mini-Cours

Transformation de Laplace : La dérivée temporelle \(d/dt\) correspond à la multiplication par la variable \(p\) (ou \(s\) dans la littérature anglo-saxonne), sous réserve de conditions initiales nulles.

Remarque Pédagogique

La mise sous forme canonique \(\frac{K}{1+\tau p}\) est cruciale : elle permet de lire directement le gain statique (valeur finale) et la constante de temps (rapidité) sans calcul supplémentaire.

Normes

Notation normalisée ISO 80000-2 : on utilise \(H(p)\) ou \(G(s)\) pour les fonctions de transfert.

Formule(s)

Transformée de la dérivée

\mathcal{L}\{\dot{x}(t)\} = p X(p) \quad (\text{si } x(0)=0)

Hypothèses

Conditions initiales nulles : on suppose que le moteur est à l'arrêt (\(\Omega(0)=0\)) au moment où on applique la tension.

Donnée(s)

Entrée	Sortie
\(U(p)\) [\( \text{V} \)]	\(\Omega(p)\) [\( \text{rad}/\text{s} \)]

Astuces

Pour mettre sous forme canonique, divisez toujours numérateur et dénominateur par le terme constant du dénominateur (ici \(Rf+K^2\)) pour faire apparaître le "1".

Schéma Avant

Calculs

Laplace

L'équation différentielle temporelle trouvée en Q1 est :

RJ \frac{\text{d}\Omega}{\text{d}t} + (Rf + K^2)\Omega = Ku

On transforme chaque terme en Laplace (\(d/dt \to p\)) et on factorise :

\begin{aligned} RJ \cdot p \cdot \Omega(p) + (Rf + K^2) \cdot \Omega(p) &= K \cdot U(p) \\ [ (RJ)p + (Rf + K^2) ] \Omega(p) &= K U(p) \end{aligned}

Fonction de Transfert Brute

On isole le rapport Sortie / Entrée :

\begin{aligned} H_{\text{BO}}(p) &= \frac{\Omega(p)}{U(p)} \\ &= \frac{K}{(Rf + K^2) + RJp} \end{aligned}

Forme Canonique

Pour avoir la forme standard \(\frac{G}{1+\tau p}\), on divise le numérateur et le dénominateur par le terme constant \((Rf + K^2)\) :

H_{\text{BO}}(p) = \frac{\frac{K}{Rf + K^2}}{1 + \frac{RJ}{Rf + K^2} p}

Schéma Après

Fonction de Transfert Canonique

Réflexions

Le gain statique dépend de \(K\), \(R\) et \(f\). Si \(f\) est faible, le gain est proche de \(1/K\).

Points de vigilance

Ne confondez pas le gain \(K\) (constante de couple) avec le gain statique \(G_{\text{BO}}\) de la fonction de transfert. Ce sont deux grandeurs différentes.

Points à Retenir

Tout moteur à courant continu (sans inductance) se comporte comme un filtre passe-bas du 1er ordre.

Le saviez-vous ?

Le contrôle en boucle ouverte est rarement utilisé pour la précision car il ne compense pas les perturbations (comme une charge qui varie sur le tapis roulant).

FAQ

Et si la vitesse initiale n'est pas nulle ?

Il faudrait ajouter un terme dépendant des conditions initiales lors de la transformation de Laplace, ou utiliser le principe de superposition.

\(H_{\text{BO}}(p) = \frac{G_{\text{BO}}}{1 + \tau_{\text{BO}} p}\)

A vous de jouer
Quelle est la dimension physique de \(\tau_{\text{BO}}\) ?

📝 Mémo
BO = Moteur seul, sans correction.

Question 3 : Fonction de Transfert Boucle Fermée (FTBF)

Principe

On ferme la boucle pour contrôler le système. On calcule la fonction de transfert globale incluant le comparateur, le correcteur proportionnel \(K_{\text{p}}\), le moteur et le retour capteur.

Mini-Cours

La contre-réaction négative : Elle consiste à soustraire la mesure de la sortie à la consigne. Cela crée un signal d'erreur \(\epsilon\) que le correcteur va chercher à annuler.

Remarque Pédagogique

La boucle fermée modifie la dynamique du système (les pôles se déplacent). Ici, le système reste du premier ordre, mais il devient plus rapide.

Normes

La représentation des schémas blocs suit la norme IEC 60050-351 relative à la commande et la régulation.

Formule(s)

Formule de Black (simplifiée)

H_{\text{BF}} = \frac{\text{Chaîne Directe}}{1 + \text{Chaîne Directe} \times \text{Retour}}

Hypothèses

On considère un retour unitaire : le capteur est supposé parfait, instantané, et de gain 1 (il ne transforme pas la valeur).

Donnée(s)

Chaîne Directe	Chaîne de Retour
\(C(p) = K_{\text{p}} \times H_{\text{BO}}(p)\)	\(B(p) = 1\)

Astuces

Astuce de calcul : Plutôt que de traîner des fractions complexes, utilisez la forme \(H_{\text{BO}} = \frac{N}{D}\). Alors \(H_{\text{BF}} = \frac{K_{\text{p}} N}{D + K_{\text{p}} N}\). C'est beaucoup plus rapide !

Schéma Avant

Architecture Boucle Fermée

Calculs

Application de Black

Posons \(H_{\text{BO}}(p) = \frac{N(p)}{D(p)}\) avec le numérateur \(N(p) = K\) et le dénominateur \(D(p) = Rf + K^2 + RJp\) (forme brute de Q2).

H_{\text{BF}}(p) = \frac{K_{\text{p}} \cdot \frac{N}{D}}{1 + K_{\text{p}} \cdot \frac{N}{D} \cdot 1}

Simplification de la fraction

On multiplie numérateur et dénominateur par \(D(p)\) pour éliminer les étages de fractions :

H_{\text{BF}}(p) = \frac{K_{\text{p}} N(p)}{D(p) + K_{\text{p}} N(p)}

Substitution finale

On remplace N et D par leurs expressions puis on regroupe les termes constants au dénominateur :

\begin{aligned} H_{\text{BF}}(p) &= \frac{K_{\text{p}} K}{(Rf + K^2 + RJp) + K_{\text{p}} K} \\ &= \frac{K K_{\text{p}}}{(Rf + K^2 + K K_{\text{p}}) + RJ p} \end{aligned}

Schéma Après

Bloc Équivalent Boucle Fermée

Réflexions

Le terme constant du dénominateur est passé de \((Rf+K^2)\) à \((Rf+K^2 + KK_{\text{p}})\). Cette augmentation du terme constant va mathématiquement réduire la constante de temps (donc accélérer le système).

Points de vigilance

Erreur classique : Oublier d'ajouter le terme \(K K_{\text{p}}\) au dénominateur lors de l'application de la formule de Black. Cela fausse tous les calculs de performance suivants.

Points à Retenir

La formule magique pour un retour unitaire : \(H_{\text{BF}} = \frac{Num_{\text{BO}}}{Den_{\text{BO}} + Num_{\text{BO}}}\).

Le saviez-vous ?

Harold Black a inventé l'amplificateur à contre-réaction en 1927 sur le trajet du ferry pour aller travailler aux Bell Labs. C'est la base de toute l'électronique moderne.

FAQ

Pourquoi réduire le gain de la boucle ?

En boucle fermée, le gain global diminue souvent par rapport à la boucle ouverte, mais on gagne énormément en bande passante (rapidité) et en stabilité face aux perturbations.

\(H_{\text{BF}}(p) = \frac{K K_{\text{p}}}{(Rf + K^2 + K K_{\text{p}}) + R J p}\)

A vous de jouer
Si le gain \(K_{\text{p}}\) tend vers l'infini, vers quelle valeur tend \(H_{\text{BF}}\) ?

📝 Mémo
BF = Gain réduit, Bande passante accrue.

Question 4 : Paramètres de l'Asservissement

Principe

L'objectif est de quantifier la performance du système. On identifie les paramètres canoniques (Gain statique \(G_{\text{BF}}\) et Constante de temps \(\tau_{\text{BF}}\)) en mettant le dénominateur sous la forme standard \(1 + \tau p\).

Mini-Cours

Constante de temps \(\tau\) : Représente l'inertie temporelle du système. C'est le temps nécessaire pour que la sortie atteigne 63% de sa valeur finale lors d'un échelon.

Remarque Pédagogique

C'est ici que l'on voit l'intérêt du correcteur proportionnel : il permet de choisir la rapidité du système en ajustant \(K_{\text{p}}\).

Normes

Les définitions de performance suivent la norme DIN 19226 pour la technologie de régulation et de commande.

Formule(s)

Forme canonique 1er ordre

H(p) = \frac{G}{1+\tau p}

Hypothèses

Le modèle linéaire établi précédemment est supposé valide sur toute la plage de fonctionnement (pas de saturation de tension).

Donnée(s)

Variable	Valeur
Gain Correcteur \(K_{\text{p}}\)	5
Résistance \(R\)	2 \(\Omega\)
Constante \(K\)	0.1
Inertie \(J\)	0.01 \( \text{kg}\cdot\text{m}^2 \)
Frottement \(f\)	0.001

Astuces

Vérifiez toujours l'unité de \(\tau\) à la fin. Elle doit être en secondes. Si vous trouvez des \(kg/V\), il y a une erreur !

Schéma Avant

Calculs

Expressions Littérales

On reprend la FTBF de Q3. On divise le numérateur et le dénominateur par le terme constant \((Rf + K^2 + KK_{\text{p}})\) pour obtenir le "1" :

G_{\text{BF}} = \frac{K K_{\text{p}}}{R f + K^2 + K K_{\text{p}}} \quad ; \quad \tau_{\text{BF}} = \frac{R J}{R f + K^2 + K K_{\text{p}}}

Calculs Numériques - Étape par étape

1. Calcul des termes individuels :

\(Rf = 2 \times 0.001 = 0.002\)
\(K^2 = 0.1 \times 0.1 = 0.01\)
\(KK_{\text{p}} = 0.1 \times 5 = 0.5\)
\(RJ = 2 \times 0.01 = 0.02\)

2. Calcul du Dénominateur Commun (terme constant) :

\begin{aligned} D &= Rf + K^2 + KK_{\text{p}} \\ &= 0.002 + 0.01 + 0.5 \\ &= 0.512 \end{aligned}

3. Calcul final des paramètres :

\begin{aligned} G_{\text{BF}} &= \frac{0.5}{0.512} \\ &\approx 0.9765 \end{aligned}

\begin{aligned} \tau_{\text{BF}} &= \frac{0.02}{0.512} \\ &\approx 0.03906 \text{ s} \end{aligned}

Schéma Après

Réponse Indicielle Théorique

Le système atteint 63% de Gbf à t = τ.

Réflexions

Le système est très rapide (39ms). L'erreur statique est faible (environ 2.4%), ce qui est excellent pour un simple correcteur P.

Points de vigilance

Attention aux ordres de grandeur. Une constante de temps mécanique pour un petit moteur est de l'ordre de 10ms à 100ms. Si vous trouvez 1000s, il y a un problème !

Points à Retenir

La boucle fermée accélère le système : \(\tau_{\text{BF}} < \tau_{\text{BO}}\).

Le saviez-vous ?

Dans un correcteur PID complet, \(K_{\text{p}}\) est le terme qui assure la réactivité immédiate ("le présent"), tandis que l'Intégrale gère la précision ("le passé") et la Dérivée l'anticipation ("le futur").

FAQ

Peut-on avoir une constante de temps négative ?

Non, jamais pour un système physique passif stable. Un \(\tau < 0\) signifierait une exponentielle divergente (\(e^{t/|\tau|}\)), donc une explosion du système (instabilité).

Résultats : \(\tau_{\text{BF}} \approx 39 \text{ ms}\) et \(G_{\text{BF}} \approx 0.976\)

A vous de jouer
Quelle est l'erreur statique en % ? (Formule : \((1 - G_{\text{BF}}) \times 100\))

📝 Mémo
Plus vite, plus fort, plus précis.

Question 5 : Analyse de la Réponse Indicielle

Principe

Calculer l'équation temporelle de la vitesse pour un échelon de commande permet de tracer la courbe de réponse et de vérifier si le cahier des charges est respecté.

Mini-Cours

La réponse indicielle est la "signature" dynamique d'un système. Elle permet de visualiser immédiatement le dépassement (s'il y en a), le temps de réponse et l'erreur statique.

Remarque Pédagogique

Il y a toujours un compromis à faire en ingénierie. Augmenter le gain améliore la précision, mais sollicite davantage l'actionneur (demande plus de tension/courant).

Normes

La définition du temps de réponse à 5% est standardisée par l'IEEE.

Formule(s)

Réponse temporelle 1er ordre

s(t) = S_{\text{final}} (1 - e^{-t/\tau})

Hypothèses

On considère un échelon de consigne parfait appliqué à \(t=0\).

Donnée(s)

Entrée	Amplitude
Échelon de consigne	\(\Omega_0\)

Astuces

Points de repère mnémotechniques : À \(t = \tau\), on est à 63%. À \(t = 3\tau\), on est à 95% (fin du régime transitoire à 5%).

Schéma Avant

Signal d'Entrée : Échelon

Calculs

Dans le domaine de Laplace, la sortie est \( \Omega(p) = H_{\text{BF}}(p) \cdot \frac{\Omega_0}{p} \). En utilisant les tables de transformées inverses, on obtient dans le domaine temporel :

\Omega(t) = \Omega_0 \cdot G_{\text{BF}} \cdot (1 - e^{-t/\tau_{\text{BF}}})

En remplaçant par les valeurs numériques trouvées précédemment :

\begin{aligned} \Omega(t) &\approx \Omega_0 \cdot 0.976 \cdot (1 - e^{-\frac{t}{0.039}}) \\ &\approx 0.976 \Omega_0 (1 - e^{-25.6 t}) \end{aligned}

Analyse qualitative : Plus \(K_{\text{p}}\) est grand, plus \(\tau_{\text{BF}}\) est petit (l'exponentielle décroît plus vite) et plus \(G_{\text{BF}}\) est proche de 1 (l'amplitude se rapproche de la consigne).

Schéma Après

Influence du Gain Kp

Visualisation de l'effet du gain sur la précision et la rapidité.

Réflexions

On constate qu'avec un simple correcteur proportionnel, on ne peut pas annuler complètement l'erreur statique (la courbe bleue n'atteint jamais la ligne rouge pointillée), mais on peut la réduire fortement.

Points de vigilance

Saturation de commande : Si \(K_{\text{p}}\) est très grand, la tension calculée par le correcteur \(u = K_{\text{p}} \epsilon\) au moment du démarrage (où l'erreur est maximale) dépassera largement la tension nominale du moteur (ex: 200V pour un moteur 24V). C'est la limite physique de ce modèle linéaire.

Points à Retenir

La réponse d'un système du 1er ordre est une convergence exponentielle monotone (sans dépassement).

Le saviez-vous ?

Le temps de réponse à 5% d'un système du premier ordre vaut exactement \(3\tau\). C'est une règle d'or pour les ingénieurs.

FAQ

Comment annuler totalement l'erreur statique ?

Il faut changer de correcteur et ajouter une action Intégrale (Correcteur PI). L'intégrateur va "accumuler" l'erreur jusqu'à ce qu'elle soit nulle.

Loi horaire : \(\Omega(t) \to \Omega_0 \cdot G_{\text{BF}}\)

A vous de jouer
A quel pourcentage de la valeur finale est-on à \(t = 3\tau\) ?

📝 Mémo
3 Tau = 95% de l'objectif.

Bilan Visuel de l'Étude

Synthèse graphique : Comparaison Boucle Ouverte vs Boucle Fermée.

📝 Grand Mémo : Synthèse Asservissement

🔑
Rôle de la rétroaction : La boucle fermée permet de corriger les erreurs, de rejeter les perturbations et d'accélérer le système, contrairement à la commande en boucle ouverte.
📐
Compromis Gain / Stabilité : Augmenter \(K_{\text{p}}\) améliore la rapidité et la précision (réduit l'erreur statique), mais risque de provoquer des dépassements, des oscillations, ou une saturation de la commande.
⚠️
Modélisation : Négliger l'inductance \(L\) simplifie le modèle (ordre 1) mais masque les potentiels pics de courant au démarrage qui pourraient endommager l'électronique.
💡
Performance : Le temps de réponse à 5% est estimé à \(3\tau\). Pour aller plus loin qu'un simple correcteur P, on utilise un PID.

"Un bon asservissement est un équilibre subtil entre nervosité (gain) et sagesse (stabilité)."

🎛️ Simulateur : Réponse Indicielle

Observez l'impact du Gain \(K_{\text{p}}\) sur la montée en vitesse du moteur.

Paramètres de commande

Gain Proportionnel \(K_{\text{p}}\) : 5

Consigne Vitesse (\(\text{rad}/\text{s}\)) : 100

Constante de temps (\(\tau_{\text{BF}}\)) : - \text{s}

Erreur statique (%) : -%

📝 Quiz final : Testez vos connaissances

1. Quel est l'effet principal d'une augmentation du gain \(K_{\text{p}}\) sur un système du 1er ordre ?

Le système devient plus lent et plus précis.
Le système devient plus rapide et plus précis.
Le système devient instable immédiatement.

2. Quelle unité correspond à la constante de temps ?

Secondes [s]
Hertz [Hz]
Radian par seconde [rad/s]

📚 Glossaire Technique

Induit: Partie rotative du moteur MCC qui reçoit le courant de puissance (rotor).
FCEM: Force Contre-Électromotrice, tension générée par la rotation du moteur qui s'oppose à la tension d'alimentation.
Asservissement: Technique automatique permettant d'amener une grandeur physique (vitesse, position) à une valeur de consigne et de l'y maintenir.
Réponse Indicielle: Réaction temporelle du système suite à un changement brusque de la consigne (échelon).
Erreur Statique: Différence permanente entre la valeur de la consigne et la valeur mesurée lorsque le régime permanent est établi.

Le Saviez-vous ?

Chargement...

Asservissement de Vitesse d’un Moteur à Courant Continu

BOÎTE À OUTILS

Titre Outil

À DÉCOUVRIR SUR LE SITE

Objectifs Pédagogiques

Données de l'étude

Fiche Technique du Moteur

Schéma Fonctionnel de l'Asservissement

Questions à traiter

Les bases théoriques

Correction : Asservissement de Vitesse d'un Moteur à Courant Continu

Question 1 : Équations Différentielles

Principe

Mini-Cours

Remarque Pédagogique

Normes

Formule(s)

Hypothèses

Donnée(s)

Astuces

Schéma Avant (Modèle Séparé)

Systèmes découplés

Calculs

Expression du courant

Substitution

Arrangement final

Schéma Après (Modèle Couplé)

Modèle Électromécanique Unifié

Réflexions

Points de vigilance

Points à Retenir

Le saviez-vous ?

FAQ

Question 2 : Fonction de Transfert Boucle Ouverte (FTBO)

Principe

Mini-Cours

Remarque Pédagogique

Normes

Formule(s)

Hypothèses

Donnée(s)

Astuces

Schéma Avant

Calculs

Laplace

Fonction de Transfert Brute

Forme Canonique

Schéma Après

Fonction de Transfert Canonique

Réflexions

Points de vigilance

Points à Retenir

Le saviez-vous ?

FAQ

Question 3 : Fonction de Transfert Boucle Fermée (FTBF)

Principe

Mini-Cours

Remarque Pédagogique

Normes

Formule(s)

Hypothèses

Donnée(s)

Astuces

Schéma Avant

Architecture Boucle Fermée

Calculs

Application de Black

Simplification de la fraction

Substitution finale

Schéma Après

Bloc Équivalent Boucle Fermée

Réflexions

Points de vigilance

Points à Retenir

Le saviez-vous ?

FAQ

Question 4 : Paramètres de l'Asservissement

Principe

Mini-Cours

Remarque Pédagogique