Contrôle Moteur par Pont en H : Analyse Transitoire
Contexte : Pilotage bidirectionnel d'un moteur à courant continu.
Le Pont en HCircuit électronique permettant d'inverser la polarité aux bornes d'un dipôle. est une structure fondamentale en électronique de puissance pour contrôler le sens de rotation des moteurs DC. Cependant, la nature inductive du moteur provoque des Phénomènes TransitoiresComportement temporaire du circuit entre deux états stables. lors des commutations, nécessitant une protection spécifique. Une maîtrise précise des constantes de temps est essentielle pour le pilotage en PWMPulse Width Modulation (Modulation de Largeur d'Impulsion)..
Remarque Pédagogique : Cet exercice vous permettra de dimensionner les composants de protection et de comprendre la réponse temporelle du courant dans le moteur, clé de la conception des onduleurs et variateurs de vitesse.
Objectifs Pédagogiques
- Analyser le fonctionnement des 4 quadrants du pont en H.
- Calculer et interpréter physiquement la constante de temps électrique \(\tau\).
- Comprendre le rôle critique des diodes de roue libre lors de l'ouverture des interrupteurs.
- Quantifier l'énergie magnétique stockée et ses risques.
Données de l'étude
On considère un moteur à courant continu alimenté par un pont en H constitué de 4 transistors idéaux. On s'intéresse à l'établissement du courant lors de la mise sous tension et à sa décroissance lors de l'arrêt.
Fiche Technique / Données
| Caractéristique | Valeur |
|---|---|
| Tension d'alimentation (\(V_{\text{cc}}\)) | 24 V |
| Résistance d'induitRésistance interne des enroulements du moteur. (\(R\)) | 2 Ω |
| Inductance d'induit (\(L\)) | 10 mH |
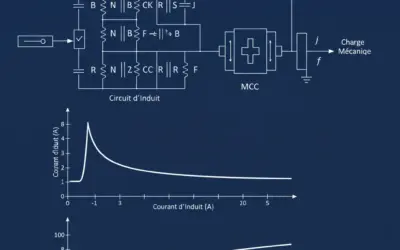
Schéma de Principe du Pont en H
| Nom du Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Tension | Vcc | 24 | V |
| Inductance | L | 10 | mH |
Questions à traiter
- Calculer l'intensité maximale du courant \(I_{\text{max}}\) en régime établi.
- Déterminer la constante de temps électrique \(\tau\) du circuit.
- Estimer le temps nécessaire pour que le courant atteigne 99% de sa valeur finale.
- Expliquer le phénomène lors de l'ouverture brutale des interrupteurs.
- Calculer l'énergie magnétique stockée dans le moteur en régime établi.
Les bases théoriques
Le circuit équivalent d'un moteur DC est constitué d'une résistance \(R\) en série avec une inductance \(L\) et une force électromotrice (fem) \(E\). Dans le cadre d'un démarrage rotor bloqué ou pour étudier la constante de temps pure, on néglige souvent \(E\) initialement ou on considère une réponse indicielle en tension. L'équation différentielle régissant le circuit est :
Réponse indicielle d'un circuit RL
La solution de cette équation différentielle pour un échelon de tension \(V_{\text{cc}}\) est une exponentielle croissante.
Équation du courant
Où :
- \(V_{\text{cc}}/R\) est la valeur asymptotique (finale) du courant.
- \(\tau\) est la constante de temps qui dicte la vitesse de convergence.
Constante de temps \(\tau\)
Elle caractérise l'inertie du système. Plus \(\tau\) est grand, plus le système est lent.
Formule de Tau
Analyse dimensionnelle : \([L]/[R] = \text{Temps}\). En effet, \(L\) s'exprime en \(V \cdot s / A\) et \(R\) en \(V / A\). Le rapport donne des secondes.
Loi de Lenz (Induction)
L'inductance s'oppose aux variations de courant en générant une tension induite.
Tension aux bornes de L
Si le courant est coupé brutalement (\(dt \to 0\)), \(di/dt \to -\infty\), donc \(u_{\text{L}}\) devient une tension négative immense (surtension), capable de détruire les composants.
Correction : Contrôle Moteur par Pont en H
Question 1 : Calcul de l'intensité maximale \(I_{\text{max}}\)
Principe
En régime établi (permanent), le courant \(i(t)\) devient constant. Par conséquent, sa dérivée par rapport au temps \(\frac{di}{dt}\) est nulle. La tension aux bornes de l'inductance \(u_{\text{L}} = L \frac{di}{dt}\) devient donc nulle : l'inductance se comporte comme un simple fil conducteur (court-circuit idéal).
Mini-Cours
En régime continu (DC steady state), les composants réactifs (L et C) ne jouent plus de rôle dynamique : L est un court-circuit, C est un circuit ouvert. Seule la résistance limite le courant.
Remarque Pédagogique
C'est le courant maximal "pire cas" que le moteur peut appeler, par exemple si on bloque son rotor au démarrage. Il sert à dimensionner l'alimentation.
Normes
Les alimentations doivent être dimensionnées pour supporter ce courant de pointe, souvent défini dans les normes CEI 60034 pour les machines tournantes.
Formule(s)
Formules utilisées
Loi d'Ohm
Hypothèses
Pour appliquer cette loi, nous posons les hypothèses suivantes :
- Régime permanent établi (\(t \to \infty\)).
- La résistance des transistors et des câbles est négligeable devant R.
Donnée(s)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Tension | Vcc | 24 | V |
| Résistance | R | 2 | Ω |
Astuces
Vérifiez toujours la puissance dissipée \(P = R I^2\) pour ne pas brûler la résistance de test ! Ici \(2 \times 144 = 288\) Watts !
Circuit Équivalent en Régime Continu
Calcul(s)
Calcul Principal
Détail du calcul
On utilise la loi d'Ohm généralisée. Puisque l'inductance est un fil parfait en régime continu (résistance nulle), la tension totale \(V_{\text{cc}}\) est appliquée uniquement aux bornes de la résistance \(R\).
On a donc : \(U = R \cdot I \Rightarrow I = \frac{U}{R}\).
En remplaçant par les valeurs numériques :
Calcul de Imax
Le courant final qui traversera le moteur et les transistors sera de 12 Ampères.
Schéma (Résultat)
Réflexions
C'est un courant important qui nécessite des transistors de puissance adaptés (ex: MOSFET de puissance, IGBT).
Points de vigilance
Attention à ne pas confondre avec le courant nominal en charge qui est souvent plus faible grâce à la force contre-électromotrice (fem \(E\)) qui s'oppose à la tension.
Points à Retenir
L'essentiel à mémoriser :
- L'inductance n'agit que pendant les variations de courant.
- En continu, seule R compte.
Le saviez-vous ?
Les moteurs de traction de TGV fonctionnent sur ce principe de base, mais pilotés par des onduleurs sophistiqués gérant des milliers d'ampères.
FAQ
Pourquoi néglige-t-on l'inductance ici ?
Car en régime constant, la dérivée du courant est nulle (\(di/dt=0\)), donc la tension aux bornes de L (\(L \cdot di/dt\)) est nulle.
A vous de jouer
Si la résistance du moteur était de 4 Ω, quel serait le courant max ?
📝 Mémo
U = RI est toujours valable aux bornes d'une résistance pure, quel que soit le régime.
Question 2 : Détermination de la constante de temps \(\tau\)
Principe
La constante de temps \(\tau\) représente l'inertie électrique du circuit. Elle ne dépend pas de la tension ou du courant, mais uniquement des propriétés physiques des composants passifs (L et R).
Mini-Cours
Dans un circuit RL série, \(\tau\) est le temps au bout duquel le courant atteint 63% de sa valeur finale lors de la charge. C'est l'inverse de la rapidité du système.
Remarque Pédagogique
Plus l'inductance L est grande, plus le système est "lourd" à démarrer. Plus la résistance R est grande, plus le système est "rapide" (car le courant final est plus faible, il est atteint plus vite).
Normes
Pas de norme spécifique pour le calcul, mais c'est une donnée critique pour définir la fréquence de hachage (PWM) qui doit être nettement supérieure à \(1/\tau\).
Formule(s)
Formules utilisées
Constante de temps
Hypothèses
L et R sont considérés constants et indépendants de la fréquence.
Donnée(s)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Inductance | L | 10 | mH |
| Résistance | R | 2 | Ω |
Astuces
N'oubliez pas de convertir les millihenrys en Henrys (x 0.001) avant de diviser !
Définition Graphique de Tau
Tau correspond à l'intersection de la tangente à l'origine avec l'asymptote finale.
Calcul(s)
Conversion(s)
Avant tout calcul, il faut convertir l'inductance en unité du système international (SI), c'est-à-dire en Henry (H).
Calcul Principal
On divise ensuite la valeur de l'inductance par celle de la résistance :
Calcul de Tau
Le résultat est en secondes. Pour plus de lisibilité, on le convertit en millisecondes (x 1000) :
Schéma (Résultat)
Réflexions
Une réponse de 5ms est assez rapide pour des applications mécaniques, mais très lente pour de l'électronique pure.
Points de vigilance
Une erreur d'unité (mH vs H) change le résultat d'un facteur 1000, ce qui fausse tout le dimensionnement du PWM.
Points à Retenir
L'essentiel à mémoriser :
- Tau = L / R
- Unité : Secondes
Le saviez-vous ?
La lettre grecque Tau est utilisée universellement pour les constantes de temps, que ce soit en électricité (RC, RL) ou en thermique.
FAQ
Est-ce que Tau dépend de la tension Vcc ?
Non, absolument pas. C'est une caractéristique intrinsèque des composants passifs (L et R). Augmenter Vcc augmentera le courant final, mais la vitesse pour atteindre 63% de ce nouveau courant sera la même.
A vous de jouer
Si L = 20 mH (R inchangé), que vaut \(\tau\) en ms ?
📝 Mémo
Tau définit la dynamique du système. Plus Tau est petit, plus le système est réactif.
Question 3 : Temps d'établissement du courant (99%)
Principe
L'équation du courant est asymptotique : mathématiquement, le courant n'atteint jamais exactement sa valeur finale \(I_{\text{max}}\). En ingénierie, on considère que le régime permanent est atteint lorsque l'erreur est négligeable (inférieure à 1%), ce qui correspond à une durée d'environ \(5\tau\).
Mini-Cours
Progression de l'exponentielle \(1 - e^{-t/\tau}\) :
- 1τ : 63.2% de la valeur finale.
- 3τ : 95.0% de la valeur finale.
- 5τ : 99.3% de la valeur finale (Régime établi).
Remarque Pédagogique
Cette règle empirique des "5 Tau" est utilisée partout en automatique et en traitement du signal.
Normes
Standard de facto en ingénierie.
Formule(s)
Formules utilisées
Critère de stabilité (99%)
Hypothèses
Système linéaire du 1er ordre soumis à un échelon.
Donnée(s)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Constante de temps | τ | 5 | ms |
Astuces
Multipliez par 5, c'est facile ! Si vous avez 5ms, ça fait 25ms.
Axe Temporel Normalisé
Calcul(s)
Démonstration Mathématique
On cherche \(t\) tel que le courant \(i(t)\) atteigne 99% de \(I_{\text{max}}\) :
On simplifie par \(I_{\text{max}}\) et on arrange l'équation :
On applique le logarithme népérien (\(\ln\)) :
D'où \(t \approx 4.605 \cdot \tau\). Par convention pratique, on arrondit à \(5\tau\). Cela confirme la règle pratique des 5τ.
Calcul Principal
Application numérique simple :
Calcul du temps
Schéma (Résultat)
Réflexions
Si on veut faire du PWM, la période de découpage doit être nettement inférieure à ce temps (ex: 10 fois plus petite, soit 2.5ms) pour que le courant n'ait pas le temps de trop varier et soit "lissé" par l'inductance.
Points de vigilance
Ne pas confondre 5 Tau (99%) et 3 Tau (95%). Certains contextes moins exigeants se contentent de 3 Tau.
Points à Retenir
L'essentiel à mémoriser :
- Règle des 5 Tau pour le régime établi.
Le saviez-vous ?
En théorie mathématique pure, l'asymptote n'est jamais atteinte (il faut un temps infini).
FAQ
Pourquoi 99% et pas 100% ?
Car la fonction \(1-e^{-x}\) ne vaut 1 que si x est infini. 99% est une convention pratique d'ingénieur.
A vous de jouer
Combien de temps pour 63% (1 Tau) ?
📝 Mémo
Le régime transitoire dure 5 Tau. Au-delà, c'est le régime permanent.
Question 4 : Phénomène d'ouverture et Protection
Principe
L'inductance impose la continuité du courant : \(i(t^-) = i(t^+)\). Elle agit comme une "masse inertielle" pour le courant. Si on ouvre brutalement un interrupteur, on force le courant à s'annuler instantanément (\(dt \to 0\)), ce qui est physiquement impossible pour une inductance chargée.
Mini-Cours
L'énergie stockée \(1/2 L I^2\) doit être évacuée quelque part. Si le circuit est ouvert, l'inductance va générer une tension suffisamment élevée pour forcer le passage du courant à travers l'isolant (air ou transistor), créant un arc électrique ou un claquage.
Remarque Pédagogique
C'est la cause n°1 de panne des cartes électroniques de puissance mal protégées.
Normes
Les principes de Compatibilité Électromagnétique (CEM) imposent aussi de gérer ces surtensions pour ne pas perturber les circuits voisins.
Formule(s)
Loi de Lenz (Auto-induction)
Hypothèses
Ouverture instantanée de l'interrupteur (\(dt \to 0\)).
Calcul Illustratif (Scénario Catastrophe)
Imaginons que l'interrupteur coupe en 1 microseconde (\(1 \text{ }\mu\text{s} = 10^{-6} \text{ s}\), très rapide) un courant de 12 A dans 10 mH.
La variation de courant est \(\Delta I = 12 - 0 = 12 \text{ A}\).
La vitesse de variation est \(\frac{\Delta I}{\Delta t} = \frac{12}{10^{-6}} = 12,000,000 \text{ A/s}\).
Calcul de la surtension
Théoriquement 120 000 Volts ! En pratique, le transistor claque bien avant (vers 60V ou 100V).
Sans Protection : Risque de Claquage
Analyse
L'interrupteur ouvert ne conduit plus. L'inductance se comporte comme une source de courant temporaire qui veut maintenir les 12 A. Il faut lui offrir un chemin de dérivation pour que le courant puisse circuler et décroître sans tout casser.
Solution Technique
Protection : Diode de Roue Libre
Réflexions
Les diodes (appelées diodes de roue libre ou *freewheeling diodes*) sont placées en anti-parallèle sur chaque transistor. Au moment de la coupure, la tension de l'inductance s'inverse, polarisant les diodes en direct. Le courant boucle alors par l'alimentation ou la masse à travers ces diodes.
Points de vigilance
Les diodes doivent être capables de supporter le même courant que le moteur (12 A) et être rapides (Fast Recovery) pour s'activer avant que la surtension ne monte !
Points à Retenir
L'essentiel à mémoriser :
- Toujours mettre des diodes de roue libre sur charge inductive.
- La diode permet la continuité du courant.
Le saviez-vous ?
C'est le même principe que l'amortisseur d'une voiture : il dissipe l'énergie du ressort pour éviter qu'il ne rebondisse indéfiniment ou ne casse la suspension.
FAQ
Une diode Zener marche-t-elle ?
Oui, elle peut servir à écrêter la tension, mais la diode de roue libre est la solution standard pour dissiper l'énergie en bouclant le courant.
A vous de jouer
Quiz : La diode conduit-elle en marche normale (moteur alimenté) ? (1=Oui, 0=Non)
📝 Mémo
Pas de DRL = Transistor mort. C'est une règle d'or.
Question 5 : Énergie Magnétique Stockée
Principe
Contrairement à une résistance qui dissipe de l'énergie, une inductance stocke de l'énergie sous forme de champ magnétique. C'est cette énergie qui doit être restituée lors de l'arrêt.
Mini-Cours
Cette énergie est emmagasinée pendant la phase de montée du courant et restituée au circuit lors de la phase de roue libre (décroissance).
Remarque Pédagogique
C'est cette énergie précise qui est responsable des étincelles sur les interrupteurs mécaniques ou de la destruction des transistors.
Normes
N/A.
Formule(s)
Énergie Inductive
Hypothèses
On considère le régime établi où le courant est maximal : \(I = I_{\text{max}} = 12 \text{ A}\).
Donnée(s)
| Paramètre | Symbole | Valeur | Unité |
|---|---|---|---|
| Inductance | L | 0.010 | H |
| Courant | I | 12 | A |
Astuces
Attention au carré sur le courant ! Si vous doublez le courant, vous quadruplez l'énergie stockée.
Stockage Magnétique (B)
Calcul(s)
Calcul Principal
Application Numérique
On élève d'abord le courant au carré : \(12^2 = 144\).
On multiplie par l'inductance : \(0.010 \times 144 = 1.44\).
On divise par 2 :
Le terme au carré a un impact majeur sur le résultat final.
Schéma (Résultat)
Réflexions
0.72 Joules peut sembler peu, mais si cette énergie doit être dissipée en 1 microseconde (\(10^{-6} \text{ s}\)), la puissance instantanée est de \(P = E/t = 0.72 / 10^{-6} = 720\,000 \text{ W}\) ! C'est cette puissance explosive qui détruit le composant.
Points de vigilance
Ne sous-estimez jamais les petites inductances traversées par de forts courants. L'énergie dépend du carré de I.
Points à Retenir
L'essentiel à mémoriser :
- L'énergie dépend du carré du courant (\(I^2\)).
- L'inductance stocke, la résistance dissipe.
Le saviez-vous ?
C'est exactement le principe utilisé dans les convertisseurs Boost pour augmenter la tension : on stocke de l'énergie dans L, puis on la "lâche" brutalement dans le circuit.
FAQ
Où va cette énergie finalement ?
Dans la phase de roue libre, elle est dissipée en chaleur (Effet Joule) dans la résistance interne du moteur et dans les diodes.
A vous de jouer
Si I double, par combien l'énergie est-elle multipliée ?
📝 Mémo
Attention à l'effet Joule lors de la dissipation.
Schéma Bilan de l'Exercice
Ce schéma résume les deux phases clés du fonctionnement : la phase active (montée du courant) et la phase de roue libre (décroissance/protection).
📝 Grand Mémo : Ce qu'il faut retenir absolument
Voici la synthèse des points clés méthodologiques et physiques abordés dans cet exercice :
-
🔑
Point Clé 1 : Inertie Inductive
Une inductance s'oppose aux variations brutales de courant. Le courant ne s'établit pas et ne s'annule pas instantanément. -
📐
Point Clé 2 : Dynamique Temporelle
La constante de temps \(\tau = L/R\) dicte la vitesse de réaction. Le régime est établi à \(5\tau\). -
⚠️
Point Clé 3 : Sécurité Absolue
Les diodes de roue libre sont obligatoires pour protéger les transistors des surtensions destructrices à l'ouverture. -
💡
Point Clé 4 : Application
Ces principes sont au cœur de la commande PWM (MLI) des moteurs modernes (voitures électriques, drones, robots).
🎛️ Simulateur interactif RL
Modifiez les paramètres Vcc et L pour observer l'impact sur la vitesse de montée du courant et sa valeur finale.
Paramètres
📝 Quiz final : Testez vos connaissances
1. Quel composant protège le transistor à l'ouverture du circuit ?
2. Si j'augmente l'inductance L du moteur, comment réagit le courant ?
📚 Glossaire
- Pont en H
- Circuit en forme de H avec 4 interrupteurs permettant d'inverser la polarité de la tension aux bornes du moteur.
- Roue Libre
- Phase de fonctionnement où le courant circule via les diodes, dissipant l'énergie magnétique stockée sans source de tension.
- Inductance
- Propriété d'un circuit à s'opposer à la variation du courant qui le traverse, mesurée en Henry (H).
- Transitoire
- État temporaire du système entre deux états stables (ex: phase de démarrage ou d'arrêt).
- PWM
- Pulse Width Modulation (Modulation de Largeur d'Impulsion), technique pour faire varier la vitesse moyenne.
Le Saviez-vous ?
Chargement...








0 commentaires